Clever breast most cancers prognosis with two-stage utilizing mammogram photographs

Clever breast most cancers detection mannequin with heuristic-assisted Trans-Res-U-Web and multi-scale DenseNet utilizing mammogram photographs

Proposed mannequin and outline

Conventional breast most cancers detection strategies like mammography, MRI, and CAD instruments regularly fail to diagnose early phases, particularly in ladies with dense breast tissues or surgical histories, resulting in misdiagnoses and pointless remedies. These strategies, whereas widespread, usually end in inaccurate predictions and may expose wholesome people to dangerous radiation. Regardless of the event of superior imaging applied sciences reminiscent of PET and Molecular Breast Imaging, their excessive prices restrict accessibility primarily to high-risk sufferers. To enhance accuracy and cut back prices, a brand new deep learning-based framework for breast most cancers detection has been launched.

Within the developed deep learning-based BC detection framework, the mammogram photographs are primarily obtained from standardized mammogram picture information sources. These uncooked photographs are then supplied to the developed ACA-ATRUNet classifier for the segmentation course of. Earlier than classification, these photographs are segmented to enhance the general accuracy of the additional detection course of. The segmented photographs are actually given to the carried out ACA-AMDN framework for classifying the BC photographs. An enhanced metaheuristic optimization algorithm referred to as the MML-EOO algorithm is recommended to scale back the processing complexity and computational time. The advisable MML-EOO algorithm optimizes the hidden neurons within the ACA-ATRUNet classifier, Epochs within the ACA-ATRUNet classifier, steps per epochs within the ACA-ATRUNet classifier, hidden neurons within the ACA-AMDN classifier, epochs within the ACA-AMDN classifier, and the batch dimension within the ACA-AMDN classifier, respectively. These optimized parameters assist in fastening your complete detection course of. The ultimate detection picture of BC is obtained from the ACA-AMDN classifier.

Atrous convolution-based attentive and adaptive breast most cancers segmentation mannequin utilizing mammogram photographs

ACA-ATRUNet-based breast most cancers segmentation

The obtained uncooked mammogram photographs (B{C}_{fs}^{img}) are given to the generated ACA-ATRUNet for picture segmentation the place (img) symbolizes photographs, (fs) implies characteristic choice. ACA-ATRUNet is developed by changing the traditional convolutional layer within the Trans-Res-UNet with an Atrous convolutional layer and together with an consideration mechanism. All the course of is repeated a number of numbers of occasions (Multi-scale) earlier than producing the ultimate segmented BC picture output (S{I}_{advert}^{TRU}). With assistance from the advisable MML-EOO algorithm, the weather within the ACA-ATRUNet construction are adjusted to extend the precision of the segmented BC photographs. The weather, reminiscent of epochs, steps per epochs, and the hidden neurons within the ACA-ATRUNet, are optimized by the prompt MML-EOO algorithm. This optimization is completed to reluimize the cube coefficient and the accuracy between the masks photographs and the segmented BC photographs. The principle concept behind this parameter optimization is mathematically represented in Eq. (1).

The time period (S1) in Eq. (1) denotes the target perform of the developed ACA-ATRUNet, (h{i}_{lm}^{TRU}) denotes the optimally adjusted variety of hidden neurons, (e{h}_{kl}^{TRU}) denotes the optimally adjusted variety of epochs, (s{e}_{jk}^{TRU}) denotes the variety of optimally adjusted steps per epoch, (Cube) signifies the cube co-efficient between the masks picture and the segmented BC picture, and (Arcy) represents the accuracy. The steps per epoch are tuned within the vary (left[text{300,1000}right]), the hidden neurons are tuned within the vary (left[text{5,255}right]), and the epochs are tuned within the vary (left[text{5,50}right]). These parameters are tuned to maximise the Cube coefficient and accuracy. The Cube coefficient is the overlap among the many masked and segmented photographs. The cube coefficient between the masks picture and the segmented picture is given by Eq. (2).

The time period (M{I}_{ma}^{am}) in Eq. (2) denotes the masks photographs and (S{I}_{advert}^{TRU}) represents the segmented BC picture. The accuracy (Arcy) evaluated utilizing Eq. (3).

In Eq. (6), the phrases (VW) characterize the true adverse, (TU) represents the true constructive, (VX) represents the false adverse, and (TV) represents the false constructive, respectively. The pictorial illustration of the carried out ACA-ATRUNEt-based BC mammogram picture segmentation is supplied in Fig. 1.

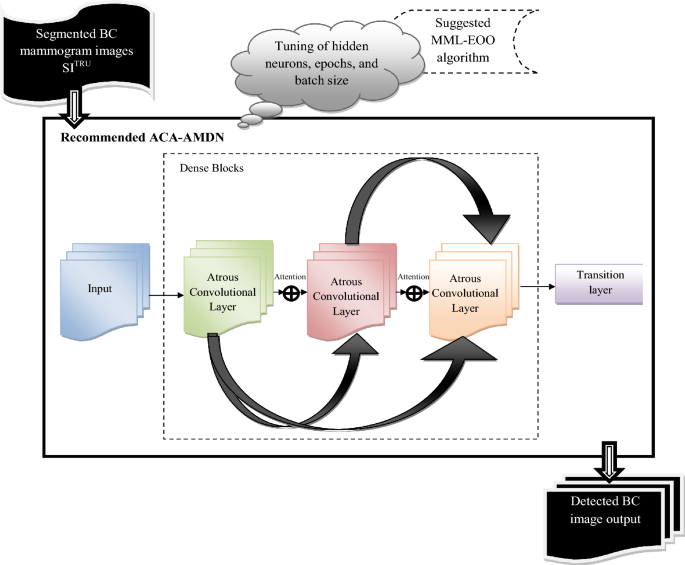
Architectural illustration of atrous convolution-based attentive and adaptive breast most cancers detection mannequin utilizing mammogram photographs

ACA-AMDN-based breast most cancers detection

The segmented photographs from the ACA-ATRUNet (S{I}_{advert}^{TRU}) are fed to the developed ACA-AMDN construction for BC picture classification. ACA-AMDN is developed by changing the traditional convolutional layer within the DenseNet with an Atrous convolutional layer and together with an consideration mechanism. The method is repeated a number of occasions (Multi-scale) within the DenseNet construction earlier than producing the ultimate classification output. The categorized picture output of BC mammogram photographs is given by (C{I}_{hs}^{MDN}). The parameters are optimized within the ACA-AMDN construction with the help of the carried out MML-EOO algorithm. The parameters like epochs, batch dimension, and the hidden neurons within the Multi-scale DenseNet are optimally tuned with the assistance of the proposed MML-EOO algorithm. This optimization goals at maximizing accuracy and minimizing False Optimistic Fee (FPR). The main contribution behind this parameter optimization is formulated as in Eq. (4)

The time period (S2) in Eq. (4) denotes the target perform of the developed ACA-AMDN, (h{i}_{ml}^{MDN}) denotes the optimally adjusted variety of hidden neurons, (e{h}_{lk}^{MDN}) denotes the optimally adjusted variety of epochs, (b{s}_{kj}^{MGN}) denotes the variety of optimally adjusted steps per epoch, and (XY) denotes the FPR. The batch dimension is tuned as (left[2, 4, 8, 16, 32, 64right]) the hidden neurons are tuned within the vary (left[5, 255right]), and the epochs are tuned within the vary (left[5, 50right]). These parameters are optimized to maximise the accuracy and decrease the FPR. The FPR is computed utilizing Eq. (5) as follows.

The pictorial illustration of the carried out ACA-AMDN-based BC classification is proven in Fig. 2.

A pictorial illustration of the carried out ACA-AMDN-based BC classification mannequin.

Proposed MML-EOO

By optimizing the epoch, hidden neurons, step dimension of Trans-Rs-UNet and epoch, hidden neurons, and batch dimension of Multi-scale DenseNet, the ultimate prediction results of the generated BC classification mannequin might be improved. The prompt MML-EOO algorithm achieves this parameter optimization. The prompt MML-EOO algorithm achieves this parameter optimization. Due to its balanced exploitation and exploration and the capability to eradicate native optimums, the EOO³¹ algorithm is used on this paper. Because of the oyster dimension choice constraint, nevertheless, this method can’t resolve difficult real-time points. Because of this, the EOO algorithm’s oyster dimension constraint (O) is upgraded utilizing the method supplied in Eq. (6).

The time period (r) in Eq. (10) represents the present iteration worth, (R) symbolizes the utmost iteration depend, and (O) denotes the dimensions of the oyster. The worth of (O) is within the vary (left[text{3,5}right]) within the conventional EOO algorithm, which is upgraded utilizing Eq. (10) within the developed MML-EOO algorithm. The worth (O) decreases linearly from 50 to 30 mm within the prompt MML-EOO algorithm. The worth (O) in Eq. (6) is used to replace the dimensions of the oyster in Eqs. 7, 8, 9, and 10. The exploration of the EO is described as follows. The quantity of vitality that’s out there within the EO (Ok) on the closing stage of searching the oyster is given by Eq. (7).

This dimension of the oyster (O) in Eq. (7) is upgraded utilizing the fitness-based idea supplied in Eq. (6). In Eq. (11),(N) denotes the present vitality requirement,(J) denotes the time requirement of the EO to open the best oyster, and (f) represents a quantity in random within the vary (left[text{0,1}right]) that’s chosen to extend the predictability within the search space. The worth of the out there vitality within the EO (Ok) varies inversely because the iteration depend (r). The place wherein the best oyster is discovered out there is supplied in Eq. (8).

The time period (Q) in Eq. (8) represents the quantity of vitality the EO obtained from consuming the best oyster of dimension (O) and ({P}_{r}) represents the place of the best oyster. The worth of (J) and the worth of (Q) depends on (O). The time required to open a specific oyster (J) is formulated as in Eq. (5).

The worth of (O) in Eq. (9) is up to date utilizing the fitness-based idea supplied in Eq. (10). The presently out there vitality within the fowl is computed as in Eq. (10).

The calorie that may be obtained by consuming the oyster (Q) is given in Eq. (11).

The worth of (Q) in Eq. (11) is up to date utilizing Eq. (6). If the time is adverse, it represents that the fowl has reached its most capability in opening the oyster and can’t additional spend vitality in opening it. That is thought of an distinctive case.(N) stays fixed within the final iteration and its previous iteration. Thus (N) and (J) can have a adverse worth. The principle contribution of the EOO algorithm is given as follows.

1. 1.

   The precision of choosing a mussel by calculating the time wanted to interrupt one is calculated utilizing the fowl’s vitality and the mussel’s dimension as variables to estimate the anticipated location of the specified meals.

2. 2.

   The random numbers entered throughout optimization assist examine new areas throughout every cycle. Keep away from an area minimal difficulty in consequence.

3. 3.

   The random numbers used at every optimization stage guarantee analysis and software.

Algorithm 1: Proposed MML-EOO pseudocode

The flowchart of the prompt MML-EOO algorithm is given in Appendix (A) supplementary info. The pseudocode of the proposed MML-EOO algorithm is offered in Algorithm 1. In our mannequin, the linear activation perform is employed within the regression-based output layers to straight output unbounded numerical values, essential for sustaining the dimensions of our goal variable. Conversely, the softmax activation perform, used within the classification layers, transforms uncooked neural community scores into possibilities, important for distinguishing amongst classes like benign, malignant, or regular in mammogram imaging. Whereas linear features assist protect output consistency, softmax is important for correct multi-class classification, facilitating definitive diagnostic choices.